Research

I am interested in the statistical, mathematical and computational aspects of methodologies for problems that arise in data science, especially for large and complex data. My research combines the following themes.

• Developing statistical methodologies for complex and high-dimensional data to make interpretable and efficient inferences by exploiting low-dimensional structures in the data.

• Constructing computationally efficient and robust algorithms for large-scale data analysis, in particular through spectral methods and convex optimization.

• Studying the theoretical aspects of the above problems within a formal statistical framework to quantify uncertainty and to better understand their non-asymptotic performance and limitations.

• Applying these methodologies to relevant scientific problems, with a special focus on neuroscience applications to understand the connectivity of the brain.

Broadly speaking, my work can be classified into three areas: statistical modeling, estimation and inference for network analysis, supervised and unsupervised machine learning methods for complex data types, and methodology and theory for pattern recognition in graphs.

The analysis of network data has received increasing attention motivated by the study of complex systems with interactive units. Examples of these systems appear in social, biological and technological networks, among others fields. My work in this area focuses in addressing estimation and inference problems by exploiting low-dimensional representations using a combination of latent space models and spectral graph inference. I have worked in developing new methodologies with provable theoretical guarantees for performing network inferences tasks including community detection, dimensionality reduction, or graph hypothesis testing, particularly for problems involving multiple networks.

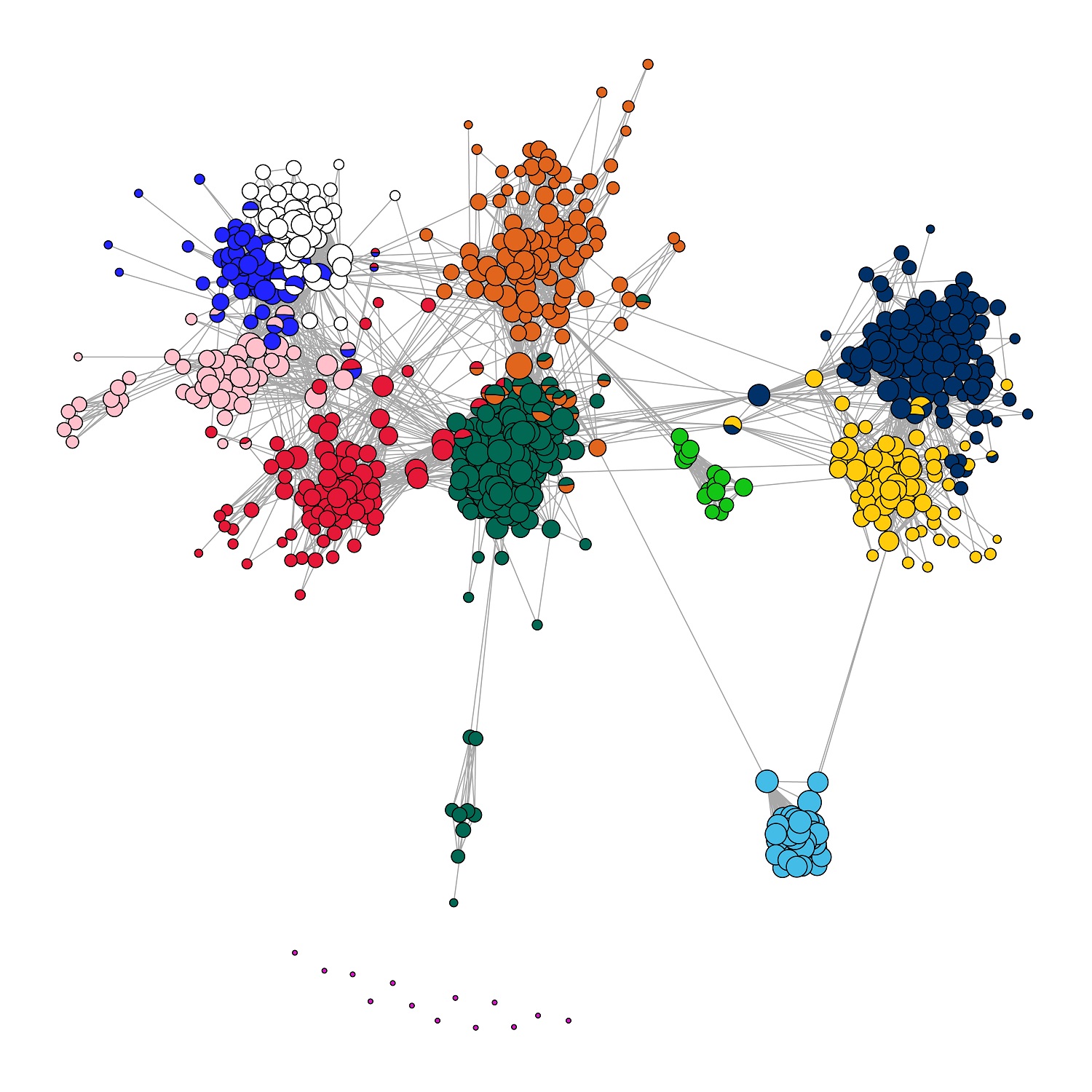
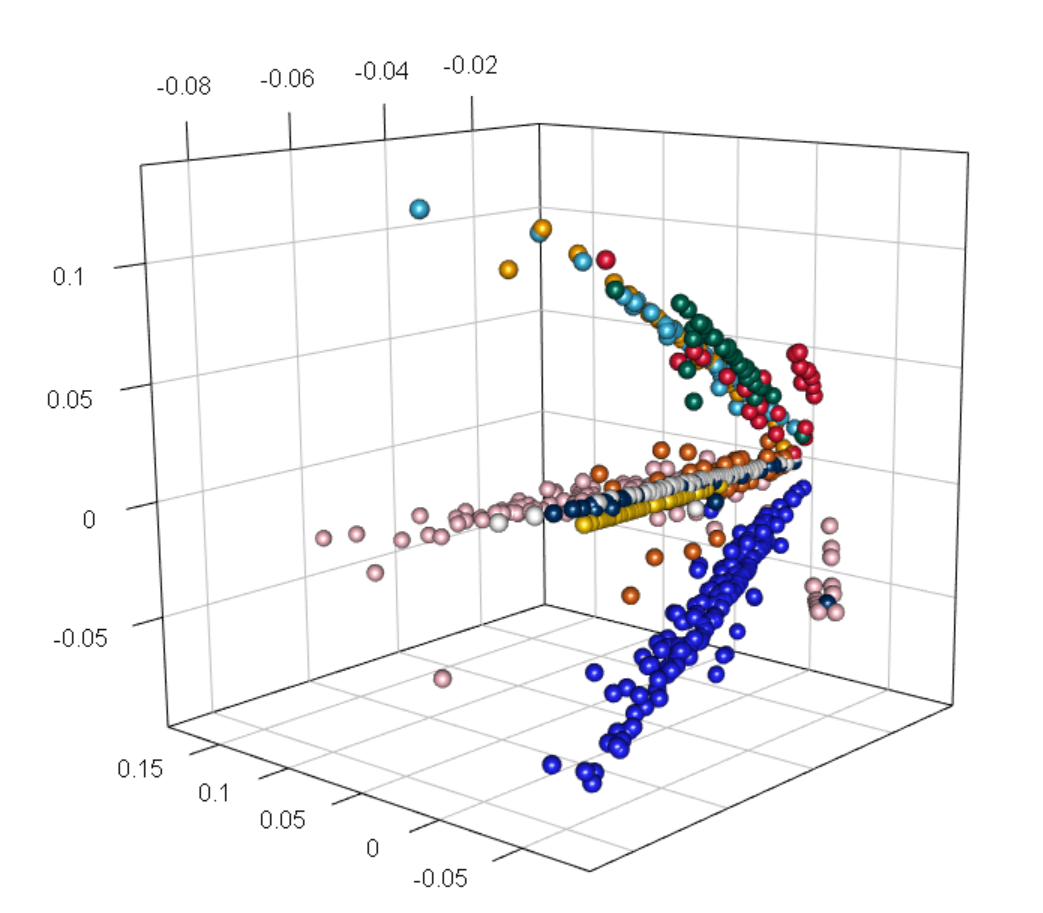
References

• Overlapping community detection in networks via sparse spectral decomposition
  Jesús Arroyo, Elizaveta Levina
  Sankhya A (Special Issue on Network Analysis) (2020), accepted pending minor revisions.
  [preprint][code]
• Inference for multiple heterogeneous networks with a common invariant subspace
  Jesús Arroyo, Avanti Athreya, Joshua Cape, Guodong Chen, Carey E. Priebe, Joshua T. Vogelstein
  Journal of Machine Learning Research (2020), to appear.
  [preprint][R code][Python code]
• Joint embedding of graphs
  Shangsi Wang, Jesús Arroyo, Joshua T. Vogelstein, Carey E. Priebe
  IEEE Transactions on Pattern Analysis and Machine Intelligence (2019), in press.
  [journal]
• Multiple Network Embedding for Anomaly Detection in Time Series of Graphs
  Guodong Chen, Jesús Arroyo, Avanti Athreya, Joshua Cape, Joshua T Vogelstein, Youngser Park, Chris White, Jonathan Larson, Weiwei Yang, Carey E Priebe
  [preprint]

Modern high-dimensional settings in statistics and machine learning are often concerned with variable selection or regularization approaches to reduce the dimension of the problem and to discover meaningful associations between variables. These tasks become more challenging in complex datasets with additional multi-scale structure in the variables, such as networks, tensors or multimodal data, which often show strong dependence associations between variables. I have worked in developing new techniques to study these problems by introducing novel regularizations and methodologies that deal with the complexity of the data effectively in supervised learning with network-valued covariates, dimensionality reduction, graphical model learning, and applications to brain network classification.

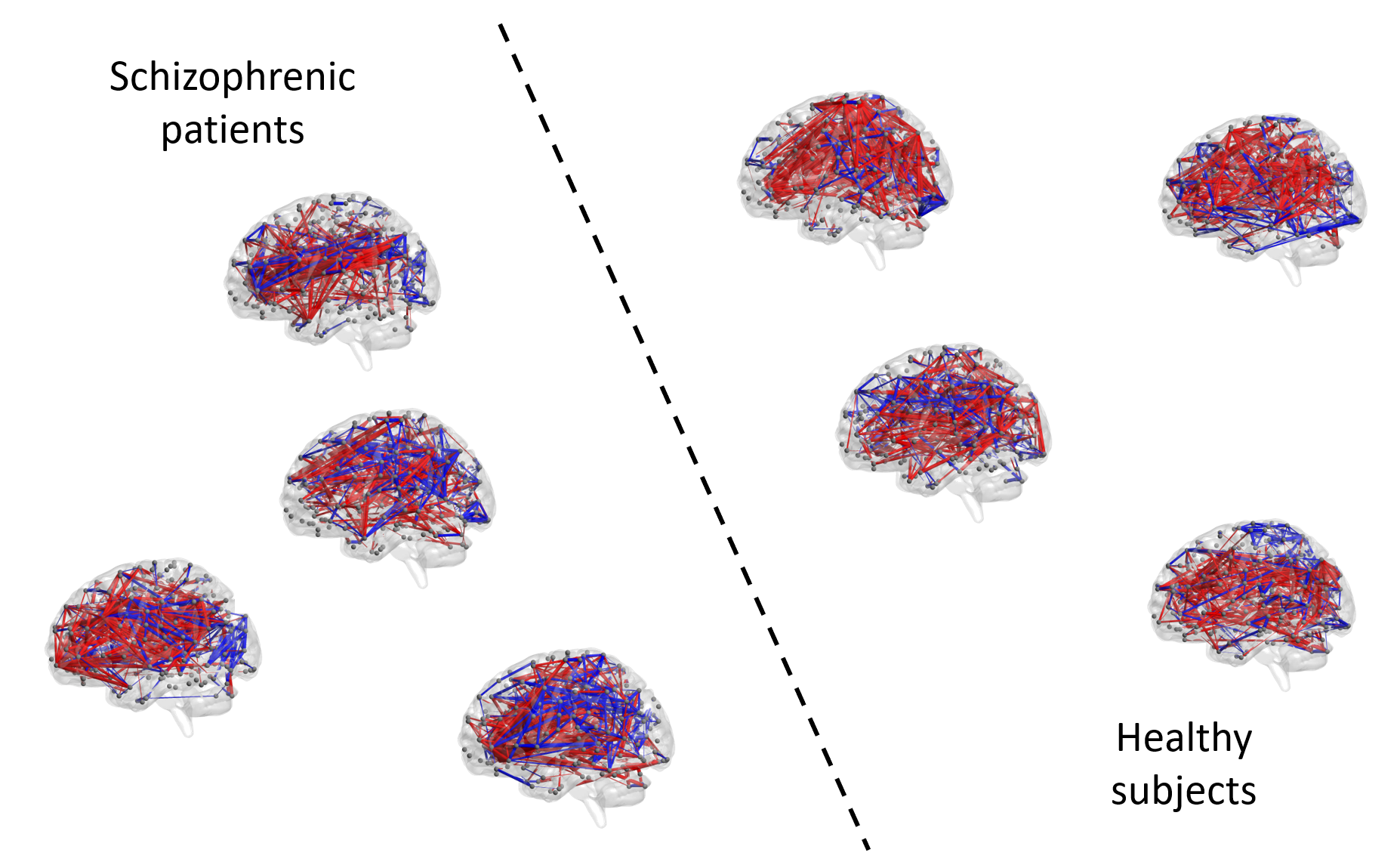
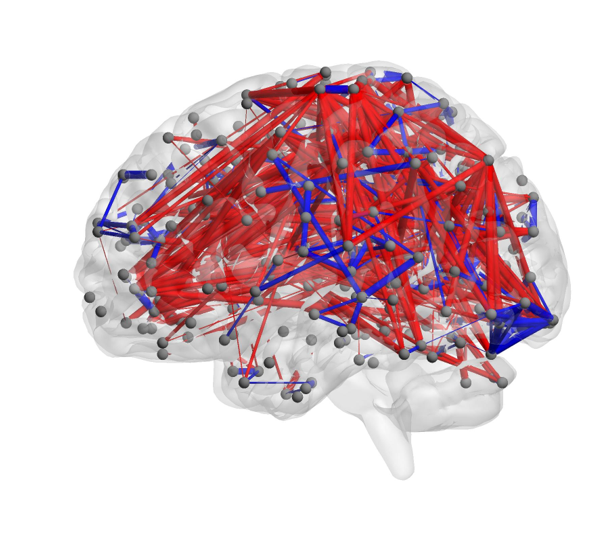
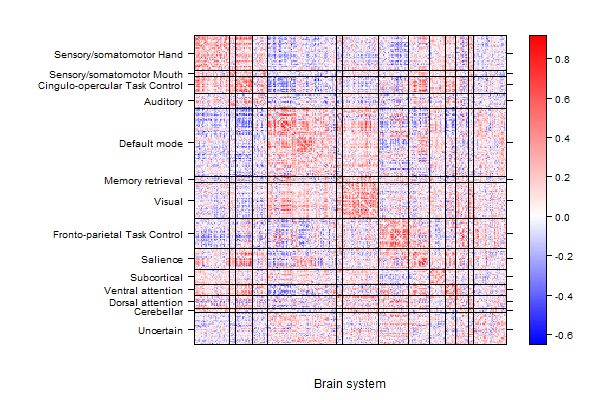
References

• Network classification with applications to brain connectomics
  Jesús D. Arroyo Relión, Daniel Kessler, Elizaveta Levina, Stephan F. Taylor
  The Annals of Applied Statistics (2019), 13(3), 1648-1677.
  [journal]
• Efficient distributed estimation of inverse covariance matrices
  Jesús Arroyo, Elizabeth Hou
  IEEE Statistical Signal Processing Workshop (SSP) (2016), pages 1-5.
  [conference proceedings]
• Simultaneous prediction and community detection for networks with application to neuroimaging
  Jesús Arroyo, Elizaveta Levina
  [preprint][code]

Identifying patterns or similarities between nodes is an important task in the study of network data. Graph matching is the problem of finding a meaningful correspondence between the nodes of two or more networks, and has applications in fields such as neuroscience, image processing or data security. Part of my work has focused in studying this problem from a statistical framework, by developing flexible and tractable statistical models and efficient computational tools, and analyzing the theoretical performance and limitations of these methodologies.

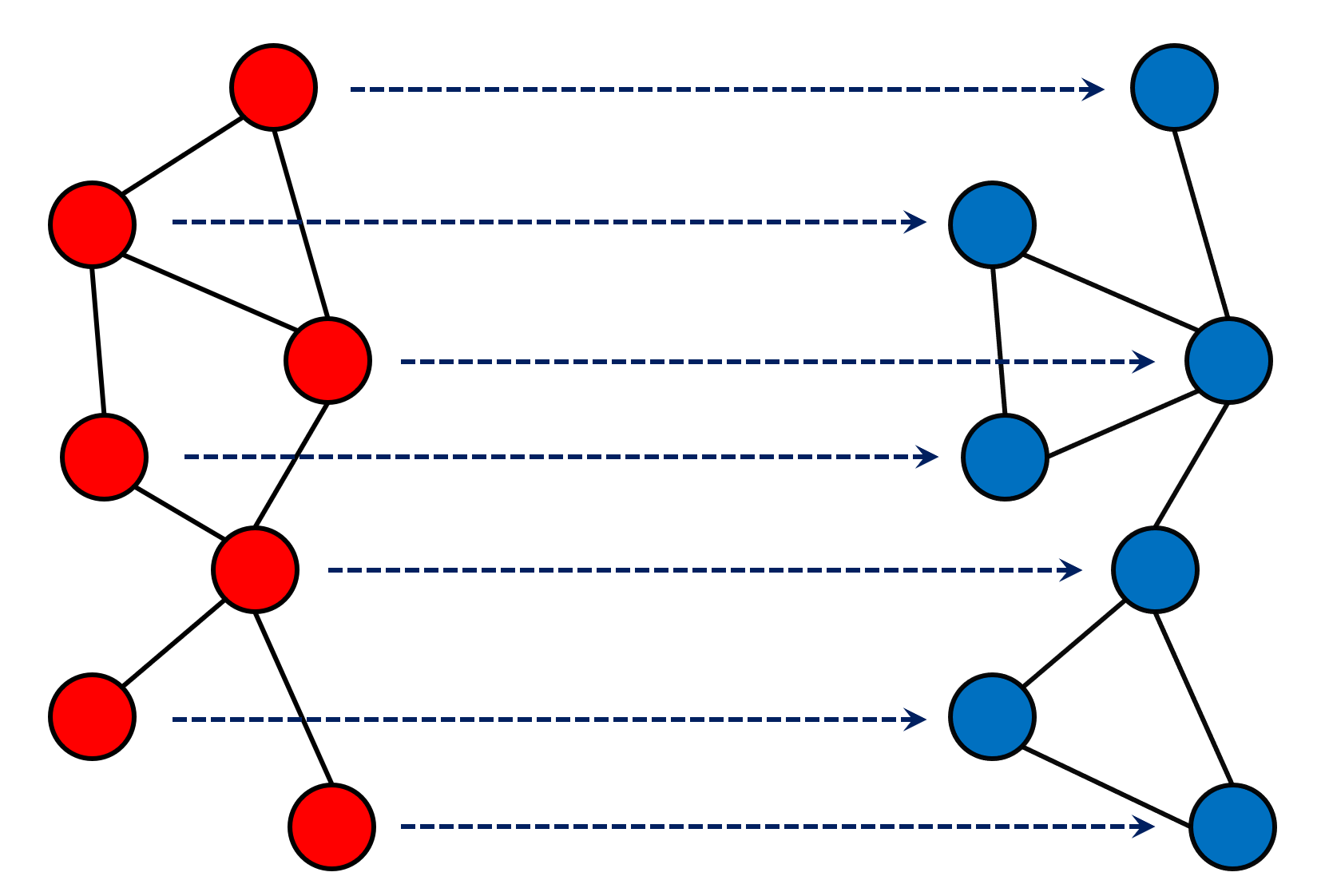
References

• Maximum Likelihood Estimation and Graph Matching in Errorfully Observed Networks
  Jesús Arroyo, Daniel L. Sussman, Carey E. Priebe, Vince Lyzinski
  Journal of Computational and Graphical Statistics (2021)
  [journal][preprint] [code]
• Graph matching between bipartite and unipartite networks: to collapse, or not to collapse, that is the question
  Jesús Arroyo, Carey E. Priebe, Vince Lyzinski
  [preprint]